テンソル積を一言でいうと,「ベクトルの組の成す空間」に相当するものです.
線形空間 $ V,W $ が与えられたとき,これらの要素(ベクトル)の組というものを考えたくなる場面が現れます.その場合2つの線形空間を個別に考えるよりも,ベクトルの組からなる線形空間を考えたほうが,様々な概念が見えやすくなります.それはちょうど2つの集合 $ A,B $ があったときに,その直積を考えることで議論がスマートになるのと似ています.
2つの線形空間の要素の組の集合 $ V\times W $ から作られる線形空間には,大きく分けて「直和」「直積」「テンソル積」の3つがあります.
では具体的に「ベクトルの組の空間」というものがどのように構成されるべきかを考えてみましょう.まず議論の起点は,2つの線形空間 $ V,W $ に対して
しかしこの段階では $ V\times W $ にはなんの演算も定義されておらず,線形空間にはなっていません.目標は2つのベクトルの組からなる「線型空間」を作ることです.演算などが何も定義されていなければ単なる集合です.
例えば現状 $V\times W$ には
そこで $ V\times W $ にどのような演算を定義すれば自然かを考えてみましょう.まず直積の要素ごとに和とスカラー倍を定義してしまう方法が考えられます.つまり
というように和とスカラー倍を定義してしまいます.このような演算を $ V\times W $ に定義した線形空間のことを $V$ と $W$ の「直和」あるいは「直積」と呼び $V\oplus W$ と書きます(無限個の線形空間を扱う場合,直和と直積は異なる概念になります).
集合の直積を思い起こすと,例えば $ A\times B $ という集合は,直積の第一成分と第二成分は別個に動き回ります.
第一成分の $ a $ を固定すると, $ \jb{(a,b)\vl b\in B} $ という集合は集合 $ B $ と自然に同一視されます:
さきほど構成した線形空間 $ V\oplus W $ は線形性の視点から見ると第一成分と第二成分が別個には動いていません.それは和やスカラー倍の定義が第一成分と第二成分で同時に行われているからです.
例えばベクトル $ v\in V $ を一つ固定したとき,
です.そもそも左辺は線形空間にすらなっていません.これは第一成分と第二成分で別個に線形性が成り立っていないことを示しています.線形空間として「ベクトルの組の空間」を名乗るならば,それは線形性が第一成分と第二成分で別個に成り立つような空間であるべきです.
すなわち, $ v\in V $ を固定したときに
これを踏まえてさきほどのように $ V\times W $ に演算を定義してみましょう.
そこでテンソル積は「もし第一成分と第二成分で別個に演算が行われる(線形性を持つ)ような線形空間が存在したらどのような性質を持っているべきか」を書き下すことによって定義します.演算は成分ごとに行われるべきなので,もし和が定義されているなら
直和のときと違うのは,和とスカラー倍が直接定義されているわけではなく,「満たすべき性質」から定義されることです.これがテンソル積というものをわかりにくくしている一つの要因だと考えられます.このような組 $ (v,w) $ を $ v\otimes w $ と書きます.
最後に残った問題があります.上のように和とスカラー倍が満たすべき性質を書きましたが,実際にこのような性質を満たす和とスカラー倍を持った線形空間を $ V $ と $ W $ から構成することができるかどうかです.現状,テンソル積は $ V\times W $ に直接演算を定義したものにはなっていません.実際,スカラー倍が満たすべき性質から
が満たされなければいけません.もしこれが直積 $ V\times W $ の元ならイコールにはならないはずです.なぜなら集合としての $ V\times W $ は第一成分と第二成分が同時に一致しているときに限り要素の等号が成り立つからです.
テンソル積は単なる $ V\times W $ ではなく, $ V\times W $ の2つの要素 $ (kv,w) $ と $ (v,kw) $ を同一視するような集合を土台として定義されるものになります.これを実現するためにテキストなどでは少しややこしい定義をしているのです.例えば次のような定義です.
$ V\times W $ の要素から生成される自由線型空間を $ F(V\times W) $ とします. $ F(V\times W) $ とは $ V\times W $ に無理やり線形空間としての演算を定義したようなもの,つまり
です.あくまでこの和 $+$ は単なる記号としての役割しかもっていません.したがって現時点で $ F(V\times W) $ の要素は一つの $ (\bullet ,\bullet) $ にまとめることはできません.
$ F(V\times W) $ は $ V\times W $ に比べて遥かに大きな線形空間になっています.この $ F(V\times W) $ に次のような同値関係を定義します.
(これは同値関係の一部で,任意の長さの形式和の同値関係 $ \sum (v\f i,w\f i)\sim \sum (v\f j,w\f j) $ は上の関係によって両辺が変形できるときと定義します.また左辺の $ + $ と右辺の $ + $ は違うものです.本来は記号を変えるべきですが,その都度変えていると大変なので同一の $ + $ 記号を使っています.)
このような同値関係で $ F(V\times W) $ を割った線形空間を $ V\otimes W $ と定義します:
例えば $ F(V\times W) $ の要素
は $ F(V\times W) $ の中で考えている限り,一つの $ (\bullet,\bullet) $ という形にまとめることはできません.しかし同値関係 $ \sim $ で $ F(V\times W) $ で割ることにより, $ F(V\times W)/\sim $ の中では
定義こそ難しいですが,一度定義できてしまえば, $ V\otimes W $ は2つのベクトルの組の空間として,演算が各成分ごとに行われるような空間として扱うことができるようになります.
現段階では $ V $ と $ W $ のテンソル積 $ V\otimes W $ において,
$ V $ と $ W $ が有限次元の場合に限って説明します. $ V $ の基底を
とします. $ V $ と $ W $ の次元はそれぞれ $ m $ と $ n $ です.このとき $ V\otimes W $ の基底がどうなるかを考えてみます.まず任意の $ v,w $ はそれぞれの基底を使って
という要素の線形結合によって書くことができます.またこれらは線型独立にもなっています.したがってこれは $ V\otimes W $ の基底になっています.すなわち $ V\otimes W $ の次元は $ m\times n $ です.
$ V\otimes W $ の和
以上により $ V\otimes W $ の基底は $ V $ の基底と $ W $ の基底の組の集合となります.線形空間の最も基本的な要素は基底であると考えると,テンソル積が「ベクトルの組の空間」の名にふさわしいものになっていると考えることができます.
結局 $ V\otimes W $ というのは,「ベクトル対の空間」と考えてOKなのです.そう考えるとあまり怖いものではないと思います.単に和とスカラー倍が成分ごとに別個に行われるような空間であるとイメージしても問題はないと思います.精密な議論のときは定義に立ち返る必要が出てきます.
テンソル積には他にも双線形写像を経由した定義もありますが,双対空間の議論も必要なのでここでは割愛したいと思います.


























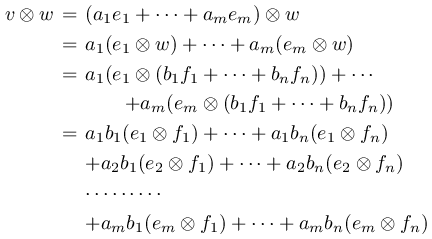


すごく参考になりました。
返信削除ありがとうございます。
ものすごく分かりやすかったです!!大変参考になりました
返信削除商空間によるテンソル積の定義について勉強しています。とても分かりやすい説明ありがとうございます。
返信削除商空間を考えるところでよく分からない点があるので教えてください。
商空間で考えれば
(v, w1) + (v, w1) - (v, w1+w2) = 0
とのことですが、この右辺の0はどのような意味なのでしょうか?
商空間を考える際の部分空間の代表元という感じなのでしょうか?
また、この式の左辺の各項も、代表元の意味なのでしょうか?
商空間の意味が十分に理解できていないので、教えていただければありがたいです。よろしくお願いします。