第1章 2次・3次・4次方程式の解の公式
●第1.1節 2次方程式●
みなさんは2次方程式の解の公式を覚えているでしょうか？ 高校数学で登場する2次方程式の解の公式とは，2次方程式
このような解の公式は，2次に限らず，3次や4次に対してもすでに与えられています．今回の記事の本題は5次方程式ですが，まずは3,4次方程式の解の公式を結果だけ見ておきます．
●第1.2節 3次方程式の解の公式●
3次方程式
です．
●第1.3節 4次方程式の解の公式●
次に4次方程式
実は求解の本質的な難しさは3次方程式とあまり変わりはありません．4次方程式の求解は2次方程式の求解2回と3次方程式の求解1回へ還元できることが分かっているのです．最終的な4つの解を書き下すと次のようになります．
ここで，u は以下の3次方程式の解の1つです：
3次方程式の解の公式はすでに得られているため，これで4次方程式の公式も得られたことになります．
●第1.4節 5次方程式にも解の公式はあるか？●
5次方程式の求解の難しさは，4次方程式とはまったく異なります．なぜなら5次方程式は一般に四則演算と冪根だけでは太刀打ちできないからです．どういうことか．実は一般の5次方程式の解の公式は
5次方程式の解の公式を求めるためには，四則演算と冪根の他に道具が必要になります．そこで登場するのが楕円積分と楕円モジュラー関数です．これを使うことによって5次方程式の解の公式を記述できることが分かっています．今回はそれを具体的に与えることを目指していきます．
結果だけを見たい方は，第5章 5次方程式の解の公式まとめをご覧下さい．
$x_1,\ldots ,x_n$を n 個の変数とします．以下で
などと書いたら，n 個の和 $x_1\ef m+\cdots +x\f n\ef m$ を表すこととします（和をとる媒介変数は常に k とします）．例えば $\Sigma(x\f k+2y\f k\ef 2)$ は
を表します．
また，$S\f m(x_\bullet)$ は $x_1,\ldots ,x_n$ に対する m 番目の基本対称式を表すものとします．つまり
です．
は複素数の範囲において，重複も含めて n 個の解を持ちます．それを $\beta\f 1,\ldots ,\beta\f n$ とします．
n 個の解の基本対称式と方程式の係数には密接な関係があります．実際 $S\f m(\beta\f\bullet)$ を $\beta\f 1,\ldots ,\beta\f n$ の m 番目の基本対称式とすると，
が成り立ちます．
ここでニュートンの恒等式を使うと，
が成り立ち，$S_m=(-1)\ef ma\thr n-m$ により次の「解の累乗和の関係式」が得られます：
5次方程式を簡単化していく過程で，解の累乗和を大量に計算する必要があるのですが，この関係式はそのときに重宝します．
この節では，これをBring-Jerrard型と呼ばれる形の5次方程式
まで簡単化していきます．
に対して， x = y - a/5 という変数変換をすることにより，
のように4次の項を消すことができます．これらの係数をそれぞれ p , q , r , s とすることにより，最初の5次方程式は
という形に簡単化されます．
から，さらに3次の項を消していきます．
4次の項を消すのとは異なり，単なる変数変換を試してみてもなかなかうまくいきません．そこで次のように考えます．
まず元の5次方程式
の5つの解を $y\f j\; (j=1,2,3,4,5)$ とし，3次の項がない5次方程式
の5つの解を $z\f j\; (j=1,2,3,4,5)$ とします．
そして，これらの解 $y\f j,z\f j$ の間に
という関係式があると仮定します．
もし α , β , A , B , C の値を，もともとの5次方程式の係数である p , q , r , s で表すことができれば，$y\f j,z\f j$の間の関係式を通じて3次の項の消去が完了します．
まず，$\Sigma z\f k$ は方程式の4次の項の係数に等しいので
です．次に $\Sigma z\f k\ef 2$ は，解の累乗和と係数の関係式により
となります．$\Sigma z\f k\ef 3$以降も同様にして，
さらにいま， $y\f k\ef 2+\alpha y\f k+\beta = z\f k$ という関係式を仮定していますから，
です．したがって
第2章 ニュートンの恒等式
●第2.1節 記号の定義●
まずは以下で用いる記号の説明をします．$x_1,\ldots ,x_n$を n 個の変数とします．以下で
また，$S\f m(x_\bullet)$ は $x_1,\ldots ,x_n$ に対する m 番目の基本対称式を表すものとします．つまり
●第2.2節 ニュートンの恒等式●
5次方程式の解の公式を求めるための準備として，ニュートンの恒等式というものを見てみます．これは5次方程式を簡単化していくときに頻繁に使用するものです．【ニュートンの恒等式】
●第2.3節 ニュートンの恒等式の代数方程式への応用●
ニュートンの恒等式を使うと，代数方程式の解の m 乗和と係数の関係を導くことができます．いま n 次方程式n 個の解の基本対称式と方程式の係数には密接な関係があります．実際 $S\f m(\beta\f\bullet)$ を $\beta\f 1,\ldots ,\beta\f n$ の m 番目の基本対称式とすると，
ここでニュートンの恒等式を使うと，
第3章 5次方程式の簡単化
今回，解の公式を与えようとする5次方程式は以下のようなものです．●第3.1節 4次の項の消去●
方程式●第3.2節 3次の項の消去●
5次方程式4次の項を消すのとは異なり，単なる変数変換を試してみてもなかなかうまくいきません．そこで次のように考えます．
まず元の5次方程式
そして，これらの解 $y\f j,z\f j$ の間に
もし α , β , A , B , C の値を，もともとの5次方程式の係数である p , q , r , s で表すことができれば，$y\f j,z\f j$の間の関係式を通じて3次の項の消去が完了します．
まず，$\Sigma z\f k$ は方程式の4次の項の係数に等しいので
左辺の $\Sigma (y\f k\ef 2+\alpha y\f k+\beta)\ef m$ の計算はかなり大変です．例えば $\Sigma (y\f k\ef 2+\alpha y\f k+\beta )\ef 2$ は次のように計算します．
式(1) , (2) の左辺を計算すると
これで $ y^5+py^3+qy^2+ry+s=0 $ と $ z^5+Az^2+Bz+C=0 $ の 2つの方程式の解の間には
また式(3)(4)(5)の左辺を計算することで次が得られます．
したがって $z^5+Az^2+Bz+C=0$ の解 $z_1,\ldots ,z_5 $に対する解の表示が得られれば，上$y\f k\ef 2+\alpha y\f k+\beta = z\f k$ を通じて $y\f 1,\ldots ,y\f 5$ が得られることになります．
これによって 考えるべき5次方程式は
●第3.3節 2次の項の消去●
ここまでで5次方程式は
まで簡単化されています．ここからさらに1次の項を消去して
という形にまで簡単化していきます．
先ほどと同様に，2つの5次方程式
のそれぞれの解を $z\f k,w\f k\; (k=1,2,3,4,5)$ とし，これらの間に
という関係があると仮定します．
4次方程式の解の公式はすでに既知のものとしていますから， P , Q , η , θ , κ , μ を A , B , C で表すことができれば1次の項の消去に成功します．
そのために，$w\f k$の累乗和を3次の項の消去のときと同じように計算していくと，
となります．
$w\f k$ と $z\f k$ の間の関係式から，
も成り立っています．したがって
先ほどと同様に，2つの5次方程式
4次方程式の解の公式はすでに既知のものとしていますから， P , Q , η , θ , κ , μ を A , B , C で表すことができれば1次の項の消去に成功します．
そのために，$w\f k$の累乗和を3次の項の消去のときと同じように計算していくと，
$w\f k$ と $z\f k$ の間の関係式から，
まずは式(6)の右辺を計算して，
つぎに式(7)の左辺を計算すると
そして式(8)の左辺を計算することにより，
これで η , θ , κ , μ の4つが A , B , C で記述できたことになります．
そして (9)(10)の右辺を計算することで，P , Q も A , B , C で記述されます．その式は最後のまとめに書くことにします．
これで P , Q , η , θ , κ , μ がすべて A , B , C で記述できました．したがって5次方程式 $z^5+Az^2+Bz+C=0$ は
●第3.4節 Bring-Jerrard型へ●
いよいよ最初の5次方程式から出発し，
これで5次方程式の簡単化は完了です．ここから先は $u^5-u+R=0$ を u について解いていくことになります．
第4章 モジュラー関数による解の表示
●第4.1節 完全楕円積分と楕円モジュラー関数●
ヤコビの楕円曲線とは，方程式
楕円曲線は母数と呼ばれるパラメータ k を変えるごとに変化しますが，それがどのような形であれ，出来上がる図形は( 複素射影平面内において)「複素トーラス」というものになることが知られています．
一般に複素トーラスは格子パラメータ τ を与えることによって決定されるものです．
母数 k と格子パラメータ τ は楕円曲線を経由して関係しています．具体的に母数 k が与えられると，それに対応する格子パラメータは
Bring-Jerrard型の5次方程式を解く際に主役となるのは， φ ( τ ) と K ( k ) です．（注：現代では楕円曲線のモジュラー関数と言ったら，ワイエルシュトラス流の j ( τ )を表していることが多いです）
●第4.2節 楕円モジュラー方程式●
φ ( Nτ ) ( N :素数) と φ ( τ ) の間には恒等的な関係式が存在します．それを楕円モジュラー方程式と呼びます．φ ( 5τ ) と φ ( τ ) の間の関係式は，5次方程式を解く際に使われます．いまパラメータ τ に対し $\tau\f j\; (j=0,1,2,\ldots )$ を
このとき，
言い換えれば，φ ( 5τ ) および $\varphi(5\tau\f j)$ は φ ( τ ) の累乗の整数倍を係数に持つ6次方程式の解になっています．これだけ見ていても，一般のBring-Jerrard型の5次方程式の解の表示にはまだ使えそうにありません．
そこで，次のような関数 J ( τ ) を定義します．
つまり J ( τ + 16n ) (n = 0 , 1 , 2 , 3 , 4 ) の5つの値は，Y の方程式
上述の Y に関する5次方程式に対して
●第4.3節 Bring-Jerrard型の求解●
X が満たす5次方程式
よって次にするべきことは，定数項が R となるような τ を求めること，すなわち
この式を変形すると，
したがって，格子パラメータ τ と母数 k の関係
いままでの流れを少し整理してみましょう．まず母数 k と格子パラメータ τ を
第5章 5次方程式の解の公式まとめ
5次方程式
ここで $x$ の式に現れる $\alpha,\beta$ はそれぞれ次のようなものです：
ここでさらに $p,q,r$ は以下のようなものです：
また， $x$ の式に現れる $z$ は以下の4次方程式の解の1つを表しています：
ここで，この方程式の係数 $\theta,\mu$ は
と表され， $\eta$ は以下の2次方程式の解の1つ：
そして $\kappa$ は以下の3次方程式の解の1つです：
さらに， $A,B,C$ は以下のようなものです：
ここで $s$ は
です．また， $z$ の方程式の右辺に現れる $u$ は
と表されています．ここで $R$ は
であり， $P,Q$ は以下のように表されています：
また， $u$ の中に現れる $J$ は
と表される関数であり，また，$K(k)$ は以下のように定義される完全楕円積分：
$\varphi(\tau)$ は以下を満たすような楕円モジュラー関数です：
参考文献
[1] V.S.Adamchik, David.J.Jeffrey, Polynomial Transformations of Tschirnhaus, Bring and Jerrard, ACM SIGSAM Bullentin, Vol37, No.3 (2003)5次方程式をBring-Jerrard型にまで簡単化する方法が説明されています．
[2] Semjon Adlaj, Multiplication and division on elliptic curves, torsion points and roots of modular equations
レベル5の楕円モジュラー多項式について参考にしました．
[3] Briot, Bouquet, Théorie des fonctions elliptiques, p654-660
楕円モジュラー方程式から5次の標準形に持っていく部分の証明が載っています．
[4] F.クライン「正20面体と5次方程式」シュプリンガー数学クラシックス
5次方程式とその周辺の詳しい話が載っている数少ない和書です
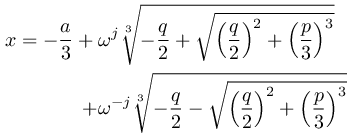
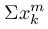
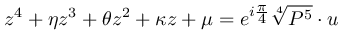
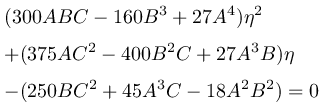
期末テストに出そうなので覚えておきます
返信削除