第0章 序説-距離とは
距離は平面あるいは空間の中の2つの点を結ぶ直線の長さと解釈されるもので,数学的には,2つの点に対して非負の実数値を定めるある種の規則のことと解釈できます.. 平面 R2 上のユークリッド距離 dE は,2点 a=(a1,a2),b=(b1,b2)∈R2 に対して
マンハッタン距離 d1 は,2点 a=(a1,a2),b=(b1,b2)∈R2 に対して
となるような関数 d1 のことです. d1 が定められた平面においては,2点の距離はすべて d1 で測ることになり,ユークリッド距離で生きてきた私たちには,なかなか馴染めない世界になるのです.例えば ( 0 , 0 ) , ( x , y ) の間の距離は
です.必ずしも,2点を結ぶ線分の(わたしたちが想像する)長さだけが距離とは限らないのです.
このように平面 R2 ひとつとっても,そこに定められる距離は千差万別です.2点に実数値を割り当てる関数で,距離と呼べるに足る性質を満たすようなものを持ってくれば,どんなへんてこなものでも距離として扱えるようになり,ユークリッド幾何において距離を使って定義していたものの類似や一般化を統一的に考えることができるようになるのです.
また,距離の概念は平面 R2 に限らず,もっと高い次元の空間 Rn ,整数,有理数などにも定めることができます.あるいはもっと抽象的に,関数の集合・結び目の集合・etc...のように,距離というものはどんな集合に対しても定めることができます.以前定義したハウスドルフ距離は R2 上の図形(コンパクト集合)の集合に対して定まっていました.つまり2点を結ぶ線分といったものが存在しないような集合に対しても距離は定まるのです.
このように平面 R2 ひとつとっても,そこに定められる距離は千差万別です.2点に実数値を割り当てる関数で,距離と呼べるに足る性質を満たすようなものを持ってくれば,どんなへんてこなものでも距離として扱えるようになり,ユークリッド幾何において距離を使って定義していたものの類似や一般化を統一的に考えることができるようになるのです.
また,距離の概念は平面 R2 に限らず,もっと高い次元の空間 Rn ,整数,有理数などにも定めることができます.あるいはもっと抽象的に,関数の集合・結び目の集合・etc...のように,距離というものはどんな集合に対しても定めることができます.以前定義したハウスドルフ距離は R2 上の図形(コンパクト集合)の集合に対して定まっていました.つまり2点を結ぶ線分といったものが存在しないような集合に対しても距離は定まるのです.
今回は R2 に定まる距離を調べ,そしてユークリッド距離とは異なる距離が定まった世界における【円】【弧長】そして【三角関数】を見ていきましょう.
曲線 C の弧長を定義する際,曲線 C を細かく分割し,それぞれの微小パーツを直線とみなすということをしていました.そして微小直線の長さを三平方の定理に従って求めていたのです.
第1節 R2 上の距離と曲線の弧長
平面 R2 上の曲線の弧長は, R2 に定められた距離によって決めることができます.曲線の弧長を定義したときのことを思い起こしてみます.曲線 C の弧長を定義する際,曲線 C を細かく分割し,それぞれの微小パーツを直線とみなすということをしていました.そして微小直線の長さを三平方の定理に従って求めていたのです.
微小直線の長さ √dx2+dy2 はユークリッド距離によって決めるものと勝手に定められており,それによって曲線全体の長さもユークリッド距離によって測られていたのです.
平面 R2 に別の距離を定めれば,微小直線の測り方も変わり,結果曲線の弧長の定義も変わってくるはずです.仮に R2 にマンハッタン距離 d1 が定められていたとしたら,微小直線の長さは
そこで R2 に一般の距離 d が定められた世界における曲線の弧長を定義してみましょう.以下,距離 d が定められた平面 R2 を (R2,d) と書くことにします. (R2,dE) と書いたらユークリッド平面を表すことになります.
第2節 (R2,d) における曲線の弧長
(R2,d) 上の曲線について考えましょう.今回は x ( t ) , y ( t ) を連続関数とします.このとき C の弧長をどのように定義すればよいのか考えてみましょう. R2 上に定められた2点間の距離のルールが,通常のユークリッド距離ではないため,弧長の定義もそれに伴って変わることになります.
距離 d によって定義される曲線の弧長のことを【 d -弧長】と呼ぶことにします.
先の話では, x ( t ) , y ( t ) を微分可能関数とし, dx , dy といった少し曖昧な対象を使って曲線の弧長を定義していましたが,今回はもう少しちゃんとした定義を与えなければなりません.なぜなら,距離 d は一般にきれいな形のものばかりではなく, dx , dy をあいまいに扱うのに限界があるからです.
例えば R2 上に
そういうわけで,もう少し汎用性のある弧長の定義が必要になるわけです.例によって厳密なものは若干面倒なところもありますが,やってみましょう.
R2 上の,実パラメータ t によって記述された曲線 C ( t ) = ( x ( t ) , y ( t ) ) ( a ≦ t ≦ b ) を n 個のパーツに分割します.パラメーター t の属する区間 [ a , b ] を n 等分割すると,それに伴って曲線 C も分割されます.
R2 上の,実パラメータ t によって記述された曲線 C ( t ) = ( x ( t ) , y ( t ) ) ( a ≦ t ≦ b ) を n 個のパーツに分割します.パラメーター t の属する区間 [ a , b ] を n 等分割すると,それに伴って曲線 C も分割されます.
[ a , b ] を分割したときの分割点は,
そして,それぞれの微小パーツの長さを距離 d によって測るものとします.
このとき微小パーツの長さすべてを足し合わせた
です. L[d] は d -弧長を表す記号とします.正確には,この極限が存在するときに限り曲線 C の d -弧長とします.
この定義は曲線 C を定義する関数 x ( t ) , y ( t ) が微分可能でなくても適用できるものですが,仮に x ( t ) , y ( t ) が微分可能だった場合は,平均値の定理により
この定義は曲線 C を定義する関数 x ( t ) , y ( t ) が微分可能でなくても適用できるものですが,仮に x ( t ) , y ( t ) が微分可能だった場合は,平均値の定理により
y の方についても同様に
第3節 平面に定める距離と弧長の式
第3.1節 Lp 距離
Lp 距離というのは, R2 の2点 (x1,y1),(x2,y2) に対して次に (R2,dp) における曲線の dp -弧長の式を考えてみましょう.先程の話から, (R2,dp) 上の曲線 C ( t ) = ( x ( t ) , y ( t ) ) ( a ≦ t ≦ b ) の dp -弧長は, x ( t ) , y ( t ) が微分可能関数であれば,
今回この曲線 S は円とは呼ばないことにします.まず,
p = ∞ のときの L∞ -距離というのは次のようなものを指しています.
であり,
第3.2節 ガリレオ距離
ガリレオ距離 dG とはこの距離によって曲線 C ( t ) = ( x ( t ) , y ( t ) ) ( a ≦ t ≦ b ) の dG -弧長は,曲線が y 軸に平行な部分のみ |y2−y1| によって測られ,それ以外は |x2−x1| で測られることになります. 具体的には次のようになります.
第3.3節 双曲距離
ユークリッド距離に対して,次のように定められる距離を考えます.この dH を双曲距離とこの記事では呼ぶことにします(一般的に使われる名称ではない).
(R2,dH) 上の曲線 C ( t ) = ( x ( t ) , y ( t ) ) ( a ≦ t ≦ b ) の dH -弧長も Lp -距離の場合と同様の考察により, x ( t ) , y ( t ) が微分可能関数であれば,
(R2,dH) 上の曲線 C ( t ) = ( x ( t ) , y ( t ) ) ( a ≦ t ≦ b ) の dH -弧長も Lp -距離の場合と同様の考察により, x ( t ) , y ( t ) が微分可能関数であれば,
第4節 単位円を再定義する
いま,平面 R2 に何かしらの距離 d:R2×R2→R≥0 が定められているとします.もちろん d は普通のユークリッド距離とは限らないものです.距離が平面に定められると,【等距離図形】という概念を考えることができるようになります.これはユークリッド距離の定められた平面において円と呼ばれているものです.
一般の (R2,d) において,原点から 1 の距離にある図形のことを【d-単位円】と呼ぶことにしましょう.
【単位円の定義】
(R2,d) の d-単位円 Cd を 例を挙げてみましょう.平面 R2 に L6 -距離
d6 の 6 の部分を 7 , 8 , 9 と上げていくと,dp-単位円はどんどん四角くなります.
d-単位円は,いかなる距離 d でも図形として現れるくれるわけではありません.例えば
d-単位円は,いかなる距離 d でも図形として現れるくれるわけではありません.例えば
のように定められた距離を考えると, d(a,b) は必ず1未満になるので, d-単位円は空集合になってしまいます.
実は単位円を一般の距離 d に対して定義できたことによって,いくつかの距離に対してそれに伴った三角関数を定義できるようになるのです.次の節でそのことについて説明してみましょう.
ユークリッド距離
実は単位円を一般の距離 d に対して定義できたことによって,いくつかの距離に対してそれに伴った三角関数を定義できるようになるのです.次の節でそのことについて説明してみましょう.
第5章 (R2,d) における三角関数
第5.1節 ユークリッド距離( L2 -距離)における三角関数
ユークリッド距離
この dE-単位円を座標 ( 1 , 0 ) から出発して dE -弧長 θ だけ進んだ点の座標が cos θ , sin θ と定義されるのでした.今回はユークリッド距離から定義される三角関数ということで,これらを cosEθ,sinEθ と書くことにしましょう.
このような定義を他の距離に対しても行うことができれば,"変な"三角関数が得られるかもしれません.
このような定義を他の距離に対しても行うことができれば,"変な"三角関数が得られるかもしれません.
第5.2節 L1 距離における三角関数
それでは,ユークリッド距離意外の距離ではどのようになるのか調べてみましょう.最初に登場していただくのはこの距離です.この世界でも三角関数を考えることができます.ユークリッド距離のときと同じように考えれば, ( 1 , 0 ) から出発して,このダイヤモンド型の単位円を反時計回りに θ だけ進んだときの座標がこの世界における cos , sin に当たるはずです.
この三角関数を cos1θ,sin1θ と表記することにします.この三角関数の特殊値を見てみましょう.
例えば, ( 1 , 0 ) から √2 だけ進むと ( 0 , 1 ) に到達するので,
例えば, ( 1 , 0 ) から √2 だけ進むと ( 0 , 1 ) に到達するので,
具体的にこの cos1θ,sin1θ をグラフに描くと下図のようになります.
この三角関数は,ユークリッド距離における三角関数と似たような性質を満たします.例えば
第5.3節 L1/2 -距離における三角関数
では, L1/2 -距離 d1/2 が定められた平面 (R2,d1/2) における三角関数はどうなるでしょうか. L1/2 -距離 d1/2 とは,この場合もいままでと同様,点 (1,0) から出発し, d1/2 -弧長 θ だけ進んだ位置にある点の座標を
ここで (1,0) から (0,1) に到達するまでの d1/2 -弧長,つまり第一象限にある単位円 C1/2 の d1/2 -弧長計算してみましょう.まず √|x|+√|y|=1 という関係式から,第一象限における C1/2 は関数
第5.4節 ガリレオ距離における三角関数
ガリレオ距離をおさらいすると,次のような関数のことを言うのでした.これに対しても単位円や三角関数を考えることができます. (R2,dG) 上の単位円は
およそ私たちが思い浮かべる円とはかけ離れたものにはなっています.
この dG-単位円上を (1,0) から出発して θ だけ進んだ座標が (cosGθ,sinGθ) と定義されます.
この dG-単位円上を (1,0) から出発して θ だけ進んだ座標が (cosGθ,sinGθ) と定義されます.
その座標はすぐに (1,θ) だということがわかります.したがって
わざわざ三角関数の記号を使うまでもないように思えますね.しかし実はガリレオ距離と次に記述する双曲距離の三角関数は,複素数に似た数体系と密接に関係しているのです.このことは次回の記事にて記述するつもりです.
第5.5節 双曲距離に対する三角関数
双曲距離を再掲しましょう.この世界での三角関数は例によって, (1,0) から出発して単位円 CH 上を
双曲距離で θ だけ進んだ点の座標と定義されます.
双曲距離で θ だけ進んだ点の座標と定義されます.
実は双曲三角関数は具体的に表示することが可能です.まず単位円 CH は |x2−y2|=1 を満たす点 (x,y) の集合なので, 0<y<x の領域に限れば,
となることがわかります.また, (cosHθ,sinHθ) は単位円 CH 上の点であることから, cos2Hθ−sin2Hθ=1 を満たします.この式を使えば cosHθ から sinHθ を求めることができ,
これら cosH,sinH を双曲三角関数とよび, cosh,sinh などと書かれます.
最後に
このように,平面上の距離の概念を変化させることによって様々な円や三角関数を見出すことができます. そして,最後の方に紹介したガリレオ距離と双曲距離における三角関数ガリレオ距離や双曲距離から定義される三角関数も,複素数と似た数体系と関係しています.そのこともいずれ.
参考文献
[1] Kevin Thompson,Tevian Dray, "Taxicab Angles and Trigonometry"
[2] Encyclopedia of Math,"Galilean Space", https://www.encyclopediaofmath.org/index.php/Galilean_space
[3] Rob Salgado (2006) "Space-Time Trigonometry"

















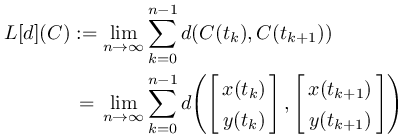










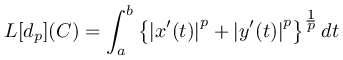





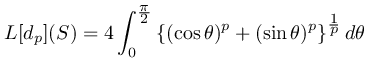

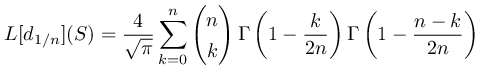



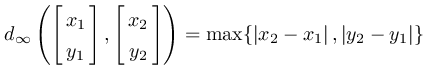













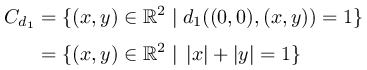









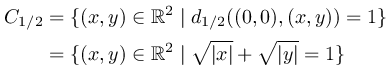











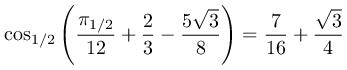






















コメント
コメントを投稿